Fractal Space Filling Curves 2002

These are a few curves I created from 1998 to 2002.

There will be more.

The Sphinx

A high order image of the four tile Sphinx curve.

There are seven versions of the Sphinx curve. Each version has a different combination of start and end points. All are required to make the complete curve.

The A curve is made of an A, a B, a D, and an F.
The B curve is made of an A, a B, a D, and an E.
The C curve is made of a B, a D, an E, and an F.
The D curve is made of an A, a B, a C, and an F.
The E curve is made of a B, two C's, and a G.
The F curve is made of an A, a B, an F and a G.
The G curve is made of a B, a C, and two G's.

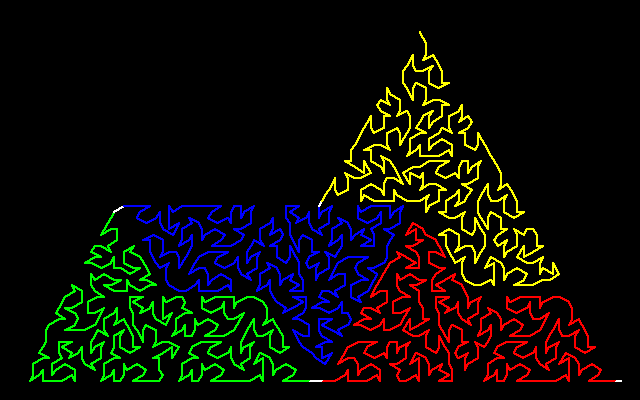
In this image the colors show how the four tiles fit together. The white parts show where the sub-tiles connect to each other. The curve winds its way through the shape once, never crossing or touching. Starting at the bottom right and ending at the top (or vice versa).

This entire shape is an A curve.
The red sub-tile is a D curve.
The green sub-tile is a B curve.
The blue sub-tile is an F curve.
The yellow sub-tile is an A curve.

Triomino

On the right is a high order Triomino curve. On the left is a lower order version showing how the four tiles fit together.

There are four versions of the Triomino curve.

The A curve is made of an A, a B, and two C's.
The B curve is made of three A's, and a B.
The C curve is made of an A, a B, a C, and a D.
The D curve is made of an A, a B, and two C's.

An Eight Tile Cross

One of my favorites. This shows the second, third, and fourth order curves. Just one version of this one, all sub-tiles are lower order mirror images of the parent.

On the left is the low order pattern of tiles, on the right is the pattern of tiles in the highest order shape.

A Twenty Seven Tile Triangle

On the top left is the pattern of tiles. This tiling is based on three tiles forming a triangle, three of those form a pattern of nine tiles, three of those form the pattern of 27 tiles. So each order of the space filling curve spans three orders of the underlying fractal tiling.

On the bottom left is the highest order shape.

On the right is the Tri-27 curve. There are five versions of this curve, each is made of some combination of the five. I like the look of this curve, but twenty seven tiles makes the program a bit messy.

A Four Tile 45 Degree Wedge

A high order version showing how the four tiles fit together.

A lower order version of the wedge. There are five versions of this curve, each is made from four of the five.

A Four Tile Star

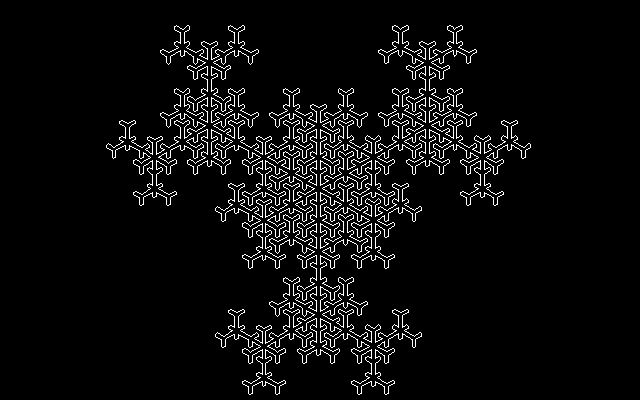
This is an unusual space filling curve. Most others are open and wind there way through the shape once, starting at one point and ending at another, and passing through each sub-tile just once.

This curve is a closed loop and each tile is drawn in an out and back fashion, starting and ending on the same sub-tile, and the curve can pass through some sub-tiles as many as six times.

This image shows the first, second, third, and fourth order curves.

On the right is the first order tiling. On the left is the second order tiling. In center is the highest order shape.

Space Filling Curves
Space Filling Curves 2002
Space Filling Curves 2009
Space Filling Curves 2010
Dragons
IFS Dragons
Interactive Turtle Tree
Interactive Sierpinski Curve
Interactive Turtle Dragon
Mandelbrot and Julia set animations
Back to Fractal Creations
Back to Home
Robot Projects
K'nex Creations
Site Index Privacy Policy Copyright Contact