Fractal Space Filling Curves
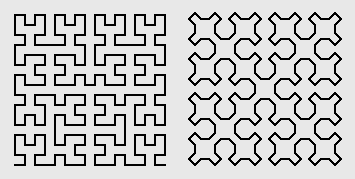
| Exquisitely convoluted, space filling curves, are created by very simple recursive procedures. These two famous examples were invented by David Hilbert (left, the Hilbert curve), and Wraclaw Sierpinski (right). |
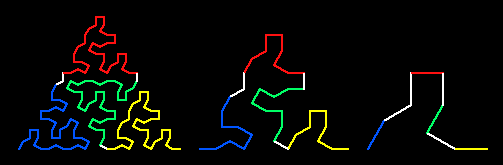
| The shapes these curves fill can be subdivided into a pattern of tiles, where each tile is similar in shape to the whole. Each tile subdivides again until you get down to the most basic shape, which is just a few lines linked so as to traverse the pattern of tiles. In this example, each more complicated version of the curve is made by replacing each colored portion with a copy of the whole curve (perhaps mirrored or rotated). |

| These three curves are based on the same lattice, or pattern of tiles, as the one above. The first (left) has long strait lines and is not a very smooth fill. The second (middle) is full of holes and so is more of a gasket than a fill. The last (right) is a true fill curve. |
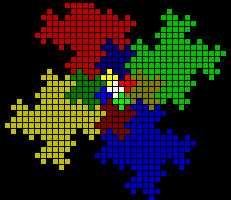
| Square tiles fit together to form a rectangular lattice. Five tiles fit together to form a cross, these cross shapes also form a rectangular lattice. Five crosses fit together to form a larger cross like shape, these cross like shapes also form a rectangular lattice. Five cross like shapes fit together to form another cross like shape... |

| The fill curve based on the above pattern should be familiar by now, its the background pattern for all of these pages. |

| One of my favorites. This right triangle subdivides into a pattern of four smaller triangles. |

Another right triangle this one divides into nine tiles.
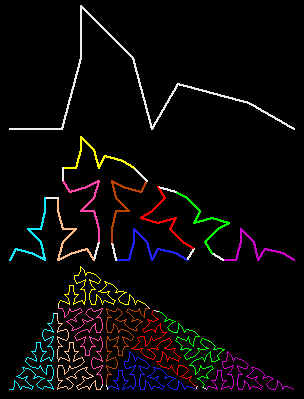
| Here you can see how higher order curves are created by inserting the next lower order curve between each line segment of the lowest order curve. |

| Another favorite, this one by Gosper is one of the most convoluted, yet one of the smoothest fills I know of. This fill is based on hexagonal tiles in a honeycomb lattice. Seven hexagons together form a six pointed shape, these in turn fit together to form a honeycomb lattice... |

|
The Sierpinski curve is based on a triangle divided into two tiles.
distorting it and making one tile smaller than the other,
makes an unusual adjustable fill curve.
I also have an interactive version of this Mutant Sierpinski Curve |

| This trapezoid filling curve is based on two interleaved tile connection patterns. |
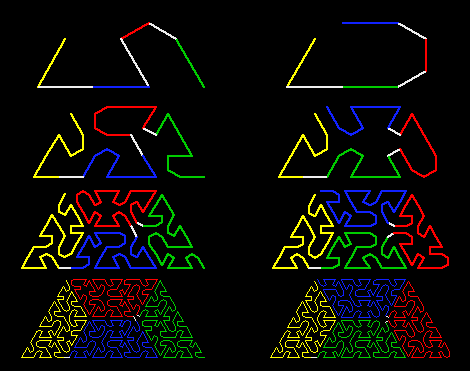
|
The curve on the right starts and ends on opposite corners.
The one on the left starts and ends on the same corner.
Each is made of three from the right (green, yellow & blue tiles),
and one from the left (red tiles).
These are just a few of the many such curves known, many more are no doubt possible. All of these images were created using turtle graphics. Most can also be made using L-systems, the lsystems directory in the Spanky Fractal Database contains several Fractint L-systems files, including many interesting space filling curves. William McWorter and I converted many of my fractal curves to L-systems for Fractint, these can be found in the file TEACHOUT.L. Also at Spanky is a Fractint L-Systems Tutorial by William McWorter, including a section on Space Filling Curves. I no longer maintain links to the files mentioned above, but they still exist and can be found by searching the web. |
Space Filling Curves
Space Filling Curves 2002
Space Filling Curves 2009
Space Filling Curves 2010
Dragons
IFS Dragons
Interactive Turtle Tree
Interactive Sierpinski Curve
Interactive Turtle Dragon
Mandelbrot and Julia set animations
Back to Fractal Creations
Back to Home
Robot Projects
K'nex Creations
Site Index Privacy Policy
Privacy Policy Copyright
Copyright Contact
Contact
Copyright 1994 -
Gary Teachout